Time : diciembre 20, 2023
Abstract: In order to make the interior structure parameter optimal, the mathematical optimization model of the ceramic bearing is set up. Based on this model, the whole optimal process is realized by iSIGHT software.The results show that this optimization has definitely instruction for ceramic bearing design.
Key words: Optimization design; iSIGHT; Bearing
With the development of the machine tool industry, the demand for spindle speed is increasing. Currently, most high-speed spindles use angular contact ball bearings with excellent rigidity and high-speed performance. For ceramic ball bearings, domestic research institutions have also conducted a lot of research and made progress, but their research mainly focuses on the processing technology of ceramic balls, the fatigue life and performance testing of ceramic bearings, and there is less research on the structural design of ceramic bearings. This article mainly focuses on the angular contact ceramic ball bearings of the 7000C series, and optimizes the main parameters using iSIGHT software.
1.1 Theoretical basis for optimized design
1.1.1 Failure mechanism of ceramic bearings
There are two forms of damage to hybrid bearings using silicon nitride (Si3N4) ceramics as rolling elements: damage to steel rings and damage to ceramic rolling elements. Both failure modes are fatigue failure, which is extremely similar to the failure mode of steel bearings. Through a large number of experiments and practical applications of hybrid ceramic bearings, it has been shown that the failure of hybrid ceramic ball bearings is mainly manifested by contact fatigue peeling of steel rings.
1.1.2 Life estimation of ceramic bearings
For ceramic bearings, whether it is the load life index, rated dynamic load C, or various correction factors, they need to be determined based on a large number of experimental results. Therefore, research on the lifespan of ceramic bearings is still limited to comparative tests with steel bearings. Due to the same failure mechanism between hybrid ceramic and steel bearings, the life relationship between hybrid ceramic ball bearings and steel ball bearings can be obtained under the premise of considering material parameters:
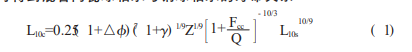
Among
![]()
In the formula: subscript c, s – ceramic bearings and steel bearings; Q – The load applied by an external load on the rolling element; Fcc – centrifugal force of ceramic balls under high-speed operating conditions; P – The external load on the bearing; C – Rated dynamic load.
1.2 Establishment of mathematical models for optimized design
1.2.1 Objective function
The objective function for optimizing the design of rolling bearings usually includes: requiring the longest fatigue life; Require the minimum rolling ratio; Require the longest wear life; Require the minimum friction torque and the maximum rated static load; Or a multi-objective function containing multiple technical indicators. Considering the characteristics of angular contact ceramic ball bearings used for high-speed spindles, such as light load and high speed, as well as the performance characteristics of ceramic bearings themselves, this article believes that the rotary ratio, wear life, and friction torque of ceramic bearings are significantly better than those of steel bearings, which is not the main contradiction to be solved. As the most important performance of ceramic bearings, fatigue life has a relatively complete prediction model as analyzed above. Therefore, this article takes the longest fatigue life of ceramic bearings as the objective function.
For ease of calculation, negative or reciprocal values are usually taken and transformed into minimization problems, which can be expressed as:
Min (f x)=min (Lc) (3)
The calculation model for the fatigue life of ceramic ball bearings can be determined by equations (1) and (2).
1.2.2 Design variables
There are many internal structural parameters of bearings, but the following main parameters play a decisive role in bearing performance: ceramic ball diameter Db, number of balls Z, center circle diameter Dm, inner groove curvature radius coefficient fi, outer groove curvature radius fe, and contact angle. For angular contact ball bearings, the original contact angle has the following geometric relationship with the radial clearance g, raceway groove curvature radius coefficient fi, fe, and ceramic ball diameter Db of the bearing:
![]()
The radial clearance g of the bearing is generally given based on the material and usage environment as known conditions, indicating that a cannot be an independent variable. Therefore, this article takes five linearly independent internal structural parameters Db, Z, Dm, fi, and fe of ceramic ball bearings as design variables, represented by a five dimensional vector as follows:
![]()
1.2.3 Constraints
During the optimization search process, the above design variables should meet a series of conditional limitations. This article mainly involves the following aspects:
![]()
In the formula, KDmin and KDmax are the minimum and maximum values of the spherical diameter coefficient, which are empirical constants related to the diameter series.
![]()
In the formula: KZ – empirical constant related to the type of cage.
![]()
1.2.4 Curvature coefficient of raceway groove
The curvature radius coefficient of the inner and outer raceway grooves of bearings has a significant impact on the stress and frictional heat generation of bearings. Under the same external load and speed conditions, the smaller the coefficient of groove curvature radius, the larger the contact area between the rolling element and the inner and outer raceways, thereby reducing the contact stress at the contact point and improving the bearing life. However, if fe and fi are too small, it will intensify the sliding friction between the rolling element and the ring raceway. Severe heat generated by friction can seriously affect bearing performance. The fi and fe of steel ball bearings are generally between 0.515 and 0.54. For ceramic ball bearings, the high elastic modulus of the ceramic ball reduces the contact area between the ball and the raceway, resulting in an increase in Hertz stress. Therefore, compared with steel bearings, the fe and fi of ceramic bearings should be appropriately reduced, so that the contact elliptical area between the ceramic ball and the groove is large enough to ensure that the service life of the bearing is not affected by high contact stress. After calculation, the reduction can be taken as 0-0.3. Due to the high centrifugal force of the rolling element under high-speed operating conditions, considering the “equal stress” and “equal strength” of the inner and outer raceways, the value of fe can be greater than fi. Therefore, this article sets the following limiting conditions for fe and fi:
Fe ≥ fi ≥ 0.505 (9)
Based on the above analysis, it can be concluded that the mathematical model for optimizing the design of ceramic ball bearings is:
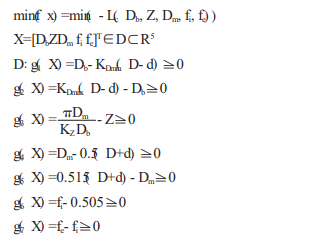
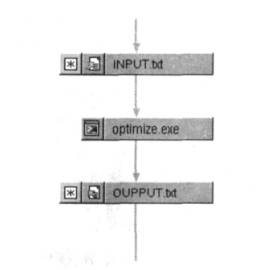
2.1 Construction of Simulation Module
Firstly, create two text files input.txt and output.txt, respectively, to save the design variables and target variables. The executable file is a console program written in VC, mainly responsible for reading the parameter values of design variables from input.txt, calculating various constraint values and target variable values according to the lifespan model, and finally writing the results of the lifespan model calculation into the output.txt file. According to the execution process of iSIGHT software, load input.txt, output.txt, and executable files as shown in Figure 1.
In order to reduce the number of iterations, the initial value of the design variables is taken as the rated value of 7007C ordinary steel bearings: ball diameter Db=8.0mm; Number of balls Z=15; Dm=48.507mm; Fi=0.515, fe=0.525.
2.2 Optimization Plan Selection
By analyzing the objective function, it can be seen that the objective function used in the article is continuous and differentiable, and the optimization design of ceramic ball bearings is a multi variable, single objective, and multi inequality constrained engineering optimization problem with both continuous and discrete variables. Based on this situation, in iSIGHT, the heuristic search in the optimization library is first selected, followed by two search steps: sequential quadratic programming (NLPQL). The NLPQL method is based on the assumption that the objective function is continuously differentiable, expanding the objective function into a second-order Laplace equation and linearizing the constraint conditions to transform it into a quadratic programming problem. The second-order equation has been improved through the equal Newton formula, and the addition of line search has improved the stability of the algorithm. The advantage of this hybrid strategy is to first use heuristic search to determine feasible areas, and then search for feasible areas.
2.3 Optimization Results
Run the optimization model according to the above steps and achieve convergence after 812 iterations. The optimized optimal design variables are: ball diameter Db=7.231mm; Number of balls Z=16; Dm=48.703mm; Fi=0.510, fe=0.521.
Taking steel bearings of the same model series as the reference object, an optimization design was carried out on ceramic bearings, an optimization model was established, and the optimization process was implemented using iSIGHT. The optimization results show that this analysis method has certain reference value for the optimization design of ceramic bearings.
When optimizing design, the material constants and empirical coefficients involved in the objective function need to be accurately determined through a large number of experiments. The selection of optimization algorithms can also have an impact on the results and result in differences in the number of iterations.
2023 December 2nd Week XZBRG Product Recommendation:
Rodamientos de rodillos cónicos de cerámica completos:
El rodamiento de rodillos cónicos de cerámica se refiere al rodamiento de rodillos de empuje radial con rodillo cilíndrico.
Pertenece al tipo de rodamiento de separación, el anillo interior y exterior del rodamiento tienen una pista de rodadura cónica.
Los rodamientos de rodillos cónicos de una hilera pueden soportar cargas radiales y cargas axiales simples.
Cuando el rodamiento soporta una carga radial, se generará una fuerza componente axial, por lo que se necesita otro rodamiento que pueda soportar la fuerza axial en la dirección opuesta para equilibrarlo.
https://www.xzballbearing.com/product/full-ceramic-tapered-roller-bearings/

Rodamiento de rodillos cónicos de una hilera de circonio